
Haydar Aguilar David de Jesús
Trasformaciones geometricas
Los objetos basicos desplegados se definen por conjuntos de puntos coordenados. Las transformaciones geometricas son procedimientos para calcular nuevas posiciones de coordenadas de estos puntos, como lo requiere un cambio especificado en tamaño y orientacion del objeto.
Translación
Una traslacion es el movimiento en linea recta de un objeto de una posicion a otra. Se traslada un punto de la posicion coordenada (x,y) a una nueva posicion (x’, y’) agregando distancias de traslacion, Tx y Ty , a las coordenadas originales: x’ = x + Tx, y’ = y + Ty El par de distancia de traslacion (Tx,Ty) se denomina tambien vector de traslacion o bien vector de cambio. Los poligonos se trasladan agrgando las distancias de traslacion especificadas a las coordenadas de cada punto extremo de la linea en el objeto.
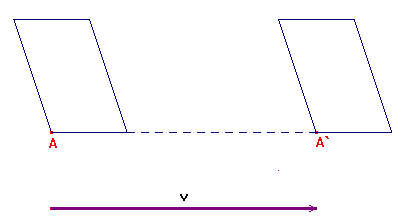
Rotación
Rotacion La transformacion de puntos de un objeto situados en trayectorias circulares se llama rotacion. Este tipo de transformacion se especifica con un angulo de rotacion, el cual determina la cantidad de rotacion de cada vertice de un poligono. El ejemplo ilustra el desplazamiento de un punto de la posicion (x,y) a la posicion (x’,y’), como lo determina un angulo de rotacion especificado relativo al origen coordenado.

Escalación
Escalacion Una transformacion para alterar el tamanio de un objeto se denomina escalacion. Esta operacion puede efectuarse con poligonos multiplicando los valores coordenados (x,y) de cada vertice de frontera por los factores de escalacion Sx y Sy para producir las coordenadas transformadas (x’, y’).
x’ = x.Sx , y’ = y.Sx El factor de escalacion Sx hace objetos a escala en la direccion x, mientras que Sy lo hace en la direccion y.

Aliasing y Anti-Aliasing
Está es una de las técnicas más importantes de hacer los gráficos y el texto, fáciles de leer y de satisfacer el ojo humano en la en pantalla es el anti-aliasing. El anti-aliasing es una manera creativa de conseguir que los contornos de la imagen aparezca liso y no con aspecto de cierra.



